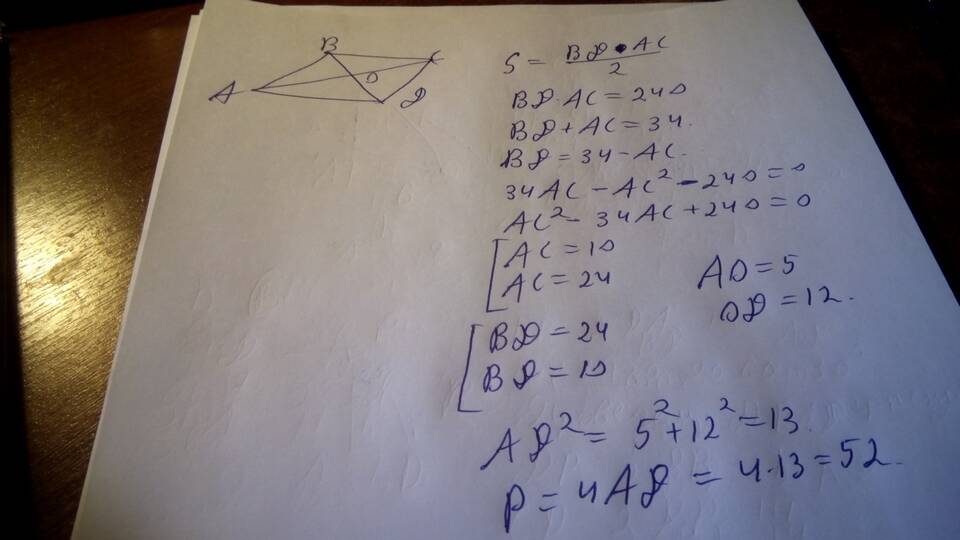
Ромб - это параллелограмм с равными сторонами, у которого диагонали обладают особыми свойствами. Рассмотрим методы вычисления суммы диагоналей этой геометрической фигуры.
Содержание
Основные свойства диагоналей ромба
- Диагонали пересекаются под прямым углом
- Точка пересечения делит диагонали пополам
- Диагонали являются биссектрисами углов
- Сумма квадратов диагоналей равна учетверенному квадрату стороны
Формулы для вычисления суммы диагоналей
| Исходные данные | Формула |
| Известны обе диагонали (d₁ и d₂) | Сумма = d₁ + d₂ |
| Известна сторона (a) и одна диагональ | Использовать соотношение: 4a² = d₁² + d₂² |
| Известна площадь (S) и одна диагональ | S = (d₁ × d₂)/2 → найти вторую диагональ |
Пошаговый алгоритм вычисления
- Определите известные параметры ромба
- Выберите подходящую формулу на основе имеющихся данных
- Если известна только одна диагональ, найдите вторую:
d₂ = 2S/d₁ или через теорему Пифагора
- Сложите длины обеих диагоналей
- Округлите результат при необходимости
Пример расчета
| Дано | Решение |
| Сторона a = 5 см | 4×5² = d₁² + d₂² → 100 = 36 + d₂² → d₂ = 8 см Сумма = 6 + 8 = 14 см |
| Одна диагональ d₁ = 6 см | |
| Найти сумму диагоналей |
Практическое применение
- В строительстве при расчете конструкций
- В дизайне при создании ромбовидных элементов
- В задачах на вычисление площади ромба
- При решении геометрических задач на свойства четырехугольников